Prev Tutorial: Contours : Getting Started
Next Tutorial: Contour Properties
Goal
- To find the different features of contours, like area, perimeter, centroid, bounding box etc
- You will learn plenty of functions related to contours.
1. Moments
Image moments help you to calculate some features like center of mass of the object, area of the object etc. Check out the wikipedia page on Image Moments
We use the function: cv.moments (array, binaryImage = false)
- Parameters
-
array raster image (single-channel, 8-bit or floating-point 2D array) or an array ( 1×N or N×1 ) of 2D points. binaryImage if it is true, all non-zero image pixels are treated as 1's. The parameter is used for images only.
Try it
From this moments, you can extract useful data like area, centroid etc. Centroid is given by the relations, \(C_x = \frac{M_{10}}{M_{00}}\) and \(C_y = \frac{M_{01}}{M_{00}}\). This can be done as follows:
2. Contour Area
Contour area is given by the function cv.contourArea() or from moments, M['m00'].
We use the function: cv.contourArea (contour, oriented = false)
- Parameters
-
contour input vector of 2D points (contour vertices) oriented oriented area flag. If it is true, the function returns a signed area value, depending on the contour orientation (clockwise or counter-clockwise). Using this feature you can determine orientation of a contour by taking the sign of an area. By default, the parameter is false, which means that the absolute value is returned.
Try it
3. Contour Perimeter
It is also called arc length. It can be found out using cv.arcLength() function.
We use the function: cv.arcLength (curve, closed)
- Parameters
-
curve input vector of 2D points. closed flag indicating whether the curve is closed or not.
Try it
4. Contour Approximation
It approximates a contour shape to another shape with less number of vertices depending upon the precision we specify. It is an implementation of Douglas-Peucker algorithm. Check the wikipedia page for algorithm and demonstration.
We use the function: cv.approxPolyDP (curve, approxCurve, epsilon, closed)
- Parameters
-
curve input vector of 2D points stored in cv.Mat. approxCurve result of the approximation. The type should match the type of the input curve. epsilon parameter specifying the approximation accuracy. This is the maximum distance between the original curve and its approximation. closed If true, the approximated curve is closed (its first and last vertices are connected). Otherwise, it is not closed.
Try it
5. Convex Hull
Convex Hull will look similar to contour approximation, but it is not (Both may provide same results in some cases). Here, cv.convexHull() function checks a curve for convexity defects and corrects it. Generally speaking, convex curves are the curves which are always bulged out, or at-least flat. And if it is bulged inside, it is called convexity defects. For example, check the below image of hand. Red line shows the convex hull of hand. The double-sided arrow marks shows the convexity defects, which are the local maximum deviations of hull from contours.
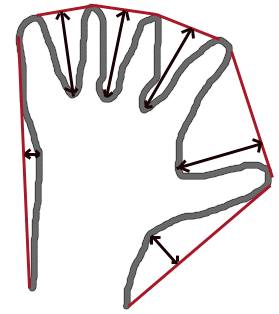
We use the function: cv.convexHull (points, hull, clockwise = false, returnPoints = true)
- Parameters
-
points input 2D point set. hull output convex hull. clockwise orientation flag. If it is true, the output convex hull is oriented clockwise. Otherwise, it is oriented counter-clockwise. The assumed coordinate system has its X axis pointing to the right, and its Y axis pointing upwards. returnPoints operation flag. In case of a matrix, when the flag is true, the function returns convex hull points. Otherwise, it returns indices of the convex hull points.
Try it
6. Checking Convexity
There is a function to check if a curve is convex or not, cv.isContourConvex(). It just return whether True or False. Not a big deal.
7. Bounding Rectangle
There are two types of bounding rectangles.
7.a. Straight Bounding Rectangle
It is a straight rectangle, it doesn't consider the rotation of the object. So area of the bounding rectangle won't be minimum.
We use the function: cv.boundingRect (points)
- Parameters
-
points input 2D point set.
Try it
7.b. Rotated Rectangle
Here, bounding rectangle is drawn with minimum area, so it considers the rotation also.
We use the function: cv.minAreaRect (points)
- Parameters
-
points input 2D point set.
Try it
8. Minimum Enclosing Circle
Next we find the circumcircle of an object using the function cv.minEnclosingCircle(). It is a circle which completely covers the object with minimum area.
We use the functions: cv.minEnclosingCircle (points)
- Parameters
-
points input 2D point set.
cv.circle (img, center, radius, color, thickness = 1, lineType = cv.LINE_8, shift = 0)
- Parameters
-
img image where the circle is drawn. center center of the circle. radius radius of the circle. color circle color. thickness thickness of the circle outline, if positive. Negative thickness means that a filled circle is to be drawn. lineType type of the circle boundary. shift number of fractional bits in the coordinates of the center and in the radius value.
Try it
9. Fitting an Ellipse
Next one is to fit an ellipse to an object. It returns the rotated rectangle in which the ellipse is inscribed. We use the functions: cv.fitEllipse (points)
- Parameters
-
points input 2D point set.
cv.ellipse1 (img, box, color, thickness = 1, lineType = cv.LINE_8)
- Parameters
-
img image. box alternative ellipse representation via RotatedRect. This means that the function draws an ellipse inscribed in the rotated rectangle. color ellipse color. thickness thickness of the ellipse arc outline, if positive. Otherwise, this indicates that a filled ellipse sector is to be drawn. lineType type of the ellipse boundary.
Try it
10. Fitting a Line
Similarly we can fit a line to a set of points. We can approximate a straight line to it.
We use the functions: cv.fitLine (points, line, distType, param, reps, aeps)
- Parameters
-
points input 2D point set. line output line parameters. It should be a Mat of 4 elements[vx, vy, x0, y0], where [vx, vy] is a normalized vector collinear to the line and [x0, y0] is a point on the line. distType distance used by the M-estimator(see cv.DistanceTypes). param numerical parameter ( C ) for some types of distances. If it is 0, an optimal value is chosen. reps sufficient accuracy for the radius (distance between the coordinate origin and the line). aeps sufficient accuracy for the angle. 0.01 would be a good default value for reps and aeps.
cv.line (img, pt1, pt2, color, thickness = 1, lineType = cv.LINE_8, shift = 0)
- Parameters
-
img image. pt1 first point of the line segment. pt2 second point of the line segment. color line color. thickness line thickness. lineType type of the line,. shift number of fractional bits in the point coordinates.
Try it
 1.9.6
1.9.6